(These guidelines are modified from materials developed by C. Caceres for IB 449 Limnology).
Introduction
Asking questions in a scientifically meaningful way
Statistics are of little use unless you first have a clear hypothesis and a specific quantitative prediction to test. Consider a simple example. You suspect that herbivores affect the amount of algae present in lake water. You make that a bit more specific and develop a general hypothesis: The presence of herbivores reduces the abundance of algae in lake water. Now you have something you can work with, but it's still a pretty vague notion. What you need to do is apply this hypothesis to a specific system. You know from surveys of local lakes that some lakes have Daphnia (large herbivorous zooplankton) whereas others do not. So, based on your hypothesis, you can now make a specific, testable prediction: The mean abundance of algae will be greater in lakes without Daphnia than in lakes where Daphnia are present. The hypothesis/prediction can be stated formally as follows:
If herbivores affect the amount of algae in lake water, then the mean abundance of algae will be greater in lakes without Daphnia than in lakes with Daphnia.
All predictions are built upon underlying assumptions.
An assumption is a condition upon which the prediction stands, but which is not directly tested. It is a fact taken for granted in an experiment. For example, you might ask whether you have to control for nutrient differences between the lakes with and without Daphnia. Answer: No, you will not be controlling for nutrients in your experimental design. So you assume that the nutrients are either the same in the lakes or that nutrients are not a factor that affects algal abundance.
If you get a significant effect of Daphnia on algal abundance, then at least one of your assumptions must have been valid. HOWEVER, when you get a non-significant result, then you examine your assumptions. Perhaps they were not valid. Perhaps no difference arose because the nutrients were not the same and nutrients were a factor that affects algal abundance. The next phase of the research would be to explicitly test the assumption (turning it into an explicit hypothesis to test next).
So try to think of any underlying factors/arguments that may be present and underpinning your prediction, but not being directly tested. Assumptions are really a part of the logical argument you are building when constructing a hypothesis/prediction.
Once you have a quantitative prediction firmly in mind for your experiment or study system, you can proceed to the next step – forming statistical hypotheses for testing. Statistical hypotheses are possible quantitative relationships among means or associations among variables. The null hypothesis states that there is no association between variables or no difference among means. For our example, it would be stated as Ho: algal abundance in Daphnia-absent lakes = algal abundance in Daphnia-present lakes (Ho: A = B). The alternative hypothesis states the pattern in the data that is expected if your predictions hold true. For our example, HA: algal abundance in Daphnia-absent lakes > algal abundance in Daphnia-present lakes (HA: A>B).
Answering your questions
Now you have to go out, gather data, and evaluate whether or not the data support your hypothesis. Our problem, essentially, is that we can't know the mean abundance of algae in ALL lakes with and without Daphnia. Instead, we have to pick a handful of each type of lake (a sample) and measure algae in each. We then calculate mean (average) algal abundance within each group of lakes and compare the two means. Inevitably one group's mean WILL be higher than the other's, just by random chance. Repeat the last sentence 10 times. If you don't understand why we asked you to repeat that sentence, ASK, this is a key aspect of the entire course.
After you have collected your data and calculated your two means (Daphnia-absent, Daphnia-present), you notice that the mean for the Daphnia-absent group appears to be higher than the mean for the Daphnia-present group. That's nice, but it doesn't tell us much. As we just got through saying 10 times over, one or the other group's mean was going to be greater even if only by random chance. Our problem is to decide, based on the data, whether the difference we observed was likely to be caused by chance alone or whether we can conclude that there probably is some real difference between the two groups.
Statistics help us make this decision by assigning p-values to tests for differences between means. P-values range between zero (impossible for difference to be due to chance) and 1 (certain that difference is due to chance). They can be thought of as the probability that the differences among means observed were caused by chance variation. If the p-value is very small (traditionally, and for this class, < 0.05), you conclude that there is some systematic difference among means. You have measured a difference that was probably NOT caused by chance. "Something else" (maybe grazing by Daphnia?) is going on. You reject the null hypothesis (Ho A = B) and claim evidence for the alternative hypothesis: (HA A>B); algal abundance was significantly greater in the Daphnia-absent lakes than in the Daphnia-present lakes. If, on the other hand, the p-value is > 0.05 there is a good chance that, if you tried the experiment again with two new samples of lakes, you would have gotten the opposite result. You have to accept the null hypothesis. You really have no strong evidence for a difference in algal abundance between the two groups of lakes.
Types of variables
There are three different types of variables: discrete, continuous and categorical. Discrete variables are those that cannot be subdivided. They must be a whole number. E.g. cats would be discrete data because there cannot be a fraction of a cat. We count or tally these data. Continuous variables are those values that cover an uninterrupted and large range of scales. A good example of a continuous variable is pH. It can be 2.4, 7.0, 8.5, etc. - any of a wide range of values between 0 and 14. Categorical variables are arbitrarily assigned by the experimenter. An example of a categorical variable is in an experiment with two treatments: you supplement a certain number of plants with nitrogen (treatment 1), and another number of plants get no nitrogen (treatment 2). So your categorical variable has two levels: nitrogen and no nitrogen. Note that categorical variables have distinct, mutually exclusive categories that lack quantitative intermediaries (e.g. present vs. absent; blonde vs. brown vs. red hair.)
Descriptive statistics
There are several commonly used descriptive statistics to use on discrete and continuous variables. These include the mean (average), variance, standard deviation, and standard error. A brief description of each follows below (Adapted from Hampton 1994).
Mean:
The mean is the sum of all the data, divided by the number of data points. In the list 10, 30, 20, the mean is 20.

Variance:
the average of the squared deviations in a sample or population. The variance considers how far each point differs from the mean. The variance for a population is denoted by σ2 and is calculated as:
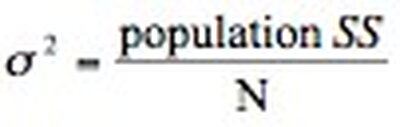
Where:
The best estimate of the population variance is the sample variance, s2:

Standard deviation: A measure of the average amount by which each observation in a series of observations differs from the mean.
Standard error: A measure of the uncertainty of the estimate of the true mean of a sample that takes into account the sample size.
SE = standard deviation / squareroot(n)
Analytical (Inferential) Statistics.
We will be using four basic statistical tools for this class: χ2 (chi-square) tests, t-tests, analysis of variance (ANOVA), and correlation (and regressions). Chi-square tests determine whether a relationship exists between two categorical variables. t-tests are used to make comparisons of mean values of 2 groups, ANOVA is used to make comparisons of mean values of >2 groups, while correlations look for associations between two continuous variables. Details about each and examples follow below.
X2test (chi-square test)(contingency test for independence)
A chi-square (χ2) test determines whether a relationship exists between two categorical variables. All other statistics (see below) apply to dependent variables that are continuous, i.e. they can take on many different values with an obvious ordering to the values (e.g. a height of 60 is greater than one of 50). Examples are: pH, height, chemical concentration).
Categorical data fall into distinct, mutually exclusive categories that lack quantitative intermediates: (present vs. absent; male vs. female; brown vs. blue vs. green eyes).
A p-value of less than 0.05 indicates that the variables are not independent; i.e. two categorical variables are related.
An example:
- We observe people to see if hair color and eye color are related. Do people with blond hair have blue eyes, etc? We develop a two-way (contingency) table to categorize each person into one group for each of the two categorical variables (e.g. brown eyes and brown hair; green eyes and red hair, etc.) We then study the table to see which combinations of variables have more or less observations than would be expected if the two variables were independent. To calculate this test, you must first find the expected value for the number of observations for each combination of the two variables based on the null hypothesis that the two variables are independent. Then you compare the differences in distribution of values for the expected and observed values.
t-tests
- A t-test is, most simply, a test to determine whether there is a significant difference between two treatment means. A p-value of less than 0.05 is usually considered to indicate a significant difference between the treatment means.
An example:
- Let's say we want to see how the presence of a predator affects the amount of food consumed by a dragonfly larva. We could set up an experiment with 10 tanks with just the dragonfly and 10 with both the dragonfly and predator (a total of two treatments). We could then measure the amount of food in each tank and use a t-test to see whether there was any difference in the mean amount of food in the 10 tanks with just dragonflies (treatment 1) and in the mean amount of food in the 10 tanks with predators (treatment 2).
ANOVA (Analysis of Variance)
- ANOVA looks for differences among treatments (like a t-test), by examining the variance around the mean. The main difference from a t-test is that ANOVA can look for differences in more than two treatment means. In fact, a t-test is really just a simple type of ANOVA. What you need to know is that if the ANOVA is significant, then there is a difference among the treatments. However, if there is a significant difference, ANOVA does not tell you anything about which treatments are significantly different from the others, and you must use other tests, such as multiple comparisons, to determine which are significantly different from the others.
An example:
- Let's modify the experiment above that had two treatments and used a t-test. Instead, we have three treatments: dragonflies alone (treatment 1), dragonflies and predator 1 (treatment 2), and dragonflies and predator 2 (treatment 3). We would use an ANOVA to see if there is a difference among the three treatments in the mean amount of food.
Correlation
- A t-test is used to test whether a difference between two group means is statistically significant. Correlations require a different kind of data. Here you have a list of subjects (individual animals, sites, ponds) and take measures of two different continuous variables for each subject. Do subjects with a high level of variable X also tend to have a high level of variable Y? These kinds of systematic associations between two variables are described by correlation.
- A correlation establishes whether there is some relationship between two continuous variables - but does not determine the nature of that relationship, i.e. it cannot be translated into cause and effect. The intensity of the relationship is measured by the correlation coefficient or "r". The value of r varies between -1 and 1. -1 indicates a strong negative relationship between the two variables, 0 indicates no relationship, and 1 a strong positive relationship.
An example:
- You suspect that there is some relationship between degrees Fahrenheit and degrees Celsius. To test this, you take an F and a C thermometer and measure water baths at 10 different temperatures. We then run a correlation using degrees F as your x variable and degrees C as your y variable, or vice versa. (For a correlation, it doesn't matter which variable is on which axis.) We would probably find a strong positive correlation - an r-value above 0.9, in this case.
- Remember - correlations only tell you that there is some association between the two variables, but not the nature of that association.
Regression
- Regression is similar to correlation, but regressions do assume that changes in one variable are predictive of changes in the other, resulting in an equation for a line. For simple linear regression, this is the old y=mx + b line (m=slope, b= y-intercept). Once this line is established, values of y can be found from values of x.
- The strength of this relationship is measured by the coefficient of determination or "R2" (the correlation coefficient squared). R2 ranges from 0 to 1.0, with 1.0 indicating that the values of x perfectly predict y (this never happens in ecology).
An example:
- We have data on light intensity and algal biomass for twenty locations within a reach of stream. We suspect that higher light intensities may lead to more algal biomass. So we could run a regression on light intensity and algal biomass, using light as our x variable and algal biomass as our y variable. We end up with an equation for the line and an R2. The R2 will probably be quite high. With a high R2 we can feel confident in using the equation for predicting values of y, based on x. In this case, we would say we could predict algal biomass based on light intensity.
- It is very important to point out, however, that although there may be a statistical relationship between the values, without an experiment, we cannot say for sure that light causes the increase in algal biomass. In other words, correlation is not causation! Although in this case, increased light most likely does result in increased algal biomass, a manipulative experiment is necessary to determine the causal relationship.
Reference:
Hampton, R.E. 1994. Introductory Biological Statistics. Wm. C. Brown Publishers. Dubuque, Iowa.
Summary: How to Choose Among Statistical Tests:
Chi-square
- (done on count data collected for two categorical variables. Do distributions differ?)
Are eye color and hair color related? Or are they independent?
Is the distribution of eye color independent of the distribution of hair color?
t-test
- (done on discrete or continuous data collected for one categorical variable with only two treatments. Do means of two treatments differ?)
Does the presence of a predator affect the amount of food consumed by a dragonfly larva?
Does the mean amount of food eaten differ in the presence vs. absence of a predator?
ANOVA
- (done on discrete or continuous data collected for one categorical variable with more than two treatments. Do means of >2 treatments differ?)
Does the predator type affect the amount of food consumed by a dragonfly larva?
Does the mean amount of food eaten differ among three predator species?
Correlation
- (done on two continuous variables; no independent-dependent variables; Is there a relationship, but no cause-effect)
Are these Fahrenheit temperatures related to these Celsius temperatures?
Regression
- (done on two continuous variables; clear independent-dependent variables; Is there a relationship, and with cause-effect)
Do higher light intensities lead to greater algal biomass?